Additional Resources
OpenStax Online Textbook
How to Read a Math Textbook
Additional Instructional Resources
Domain and Range of a Function
Summary
A function is a mapping from a set of inputs to a set of outputs with exactly one output for each input.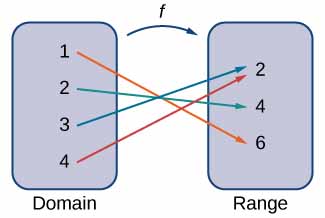
A function maps every element in the domain to exactly one element in the range. Although each input can be sent to only one output, two different inputs can be sent to the same output.
We can also visualize a function by plotting points (x,y) in the coordinate plane where y=f(x). The graph of a function is the set of all these points. For example, consider the function f, where the domain is the set D={1,2,3} and the rule is f(x)=3−x. In Figure, we plot a graph of this function.>
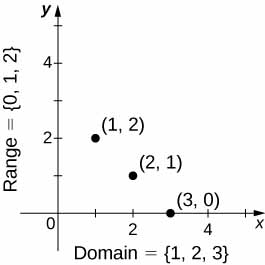
Here we see a graph of the function f with domain {1,2,3} and rule f(x)=3−x. The graph consists of the points (x,f(x)) for all x in the domain.
For certain functions, such as and , the domains are sets with an infinite number of elements. Clearly we cannot list all these elements. When describing a set with an infinite number of elements, it is often helpful to use one of the following types of notation:
Interval Notation
This is read: "all numbers greater than and less than ". In this form of notation, and are called the endpoints of the set.
If we want to consider the set that includes the endpoints, we would denote this set by writing
Set Builder Notation
This is read: "set of real numbers such that ."
Example:
The set of real numbers such that is greater than and less than