Additional Resources
OpenStax Online Textbook
How to Read a Math Textbook
Additional Instructional Resources
Logarithmic Differentiation
Objectives
- Find the derivative of logarithmic functions.
- Use logarithmic differentiation to determine the derivative of a function.
Summary
Logarithmic differentiation is a technique that allows us to differentiate a function by first taking the natural logarithm of both sides of an equation, applying properties of logarithms to simplify the equation, and differentiating implicitly. For example, logarithmic differentiation allows us to differentiate functions of the form or very complex functions. Note that variable now plays a role in the exponent, hence the reason to take the natural logarithm of both sides of the equation to bring the variable down to the base and then apply the regular differentiation rules.
Problem
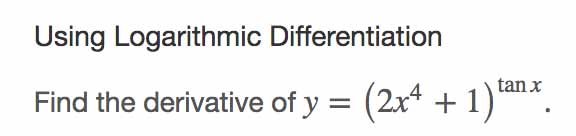
Solution
Using Logarithmic differentiation find the derivative of the function.
- Step 1 Take the natural logarithm of both sides.
- Step 2 Expand using properties of logarithms.
- Step 3 Differentiate both sites. Use the product rule on the right.
- Step 4 Multiply by Y on both sides. Step 5 Substitute y equals 2x^4 + 1, all raised to the exponent tangent x.